generic tetromino game

The basics

The visible playfield contains 20 rows, each row fitting 10 tiles, making a total of 200 tiles. The rows are numbered from 0 to 19 top to bottom; the columns are numbered from 0 to 9 left to right. So far pretty straightforward.

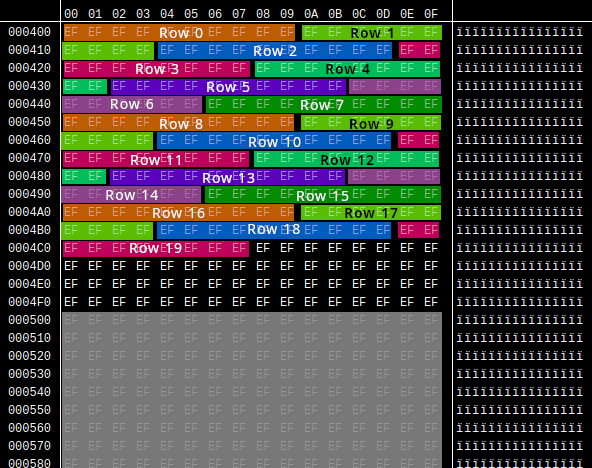
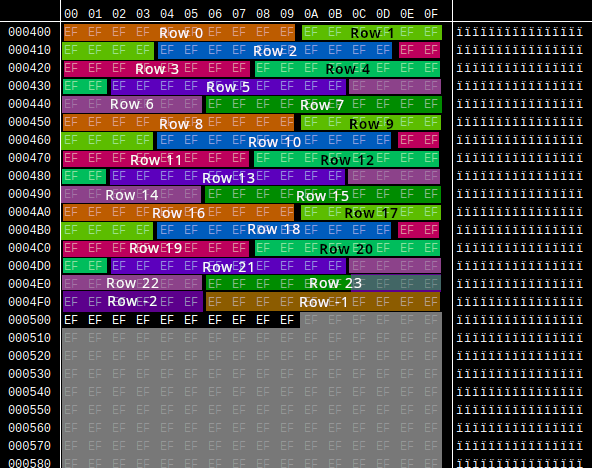
The board is stored at $0400 in-memory, as an array of 200 bytes (ok, actually it's more complicated than this, but we'll get there. I'm trying to keep things simple for now). Each byte contains the ID of one tile on the board. Unfilled tiles are represented by $EF -- the black tile. Filled tiles are represented by $7B, $7C, or $7D, depending on the specific graphic used.

Whenever a row is cleared, the game shifts all data preceding the cleared row by 10, and then fills the top row with $EF. In C, this might look something like this:

memmove(&board[10], &board[0], cleared_row * 10);
memset(&board[0], 0xEF, 10);

The above C code isn't actually what the game does, but we'll get to that when we get to that. This oversimplification works for now.

Recall that each row has 10 columns, so shifting by 10 effectively moves everything down by exactly one row. This process is repeated for each row that's cleared (from top to bottom).

The bottom-most row that can be cleared is, well, the bottom-most row: row 19. It follows that row 19 can't ever be shifted in normal gameplay, so we surely will never need to worry about anything being shifted out of bounds. All is well.

just kidding hahahahahahahahahahaha

Negative indices

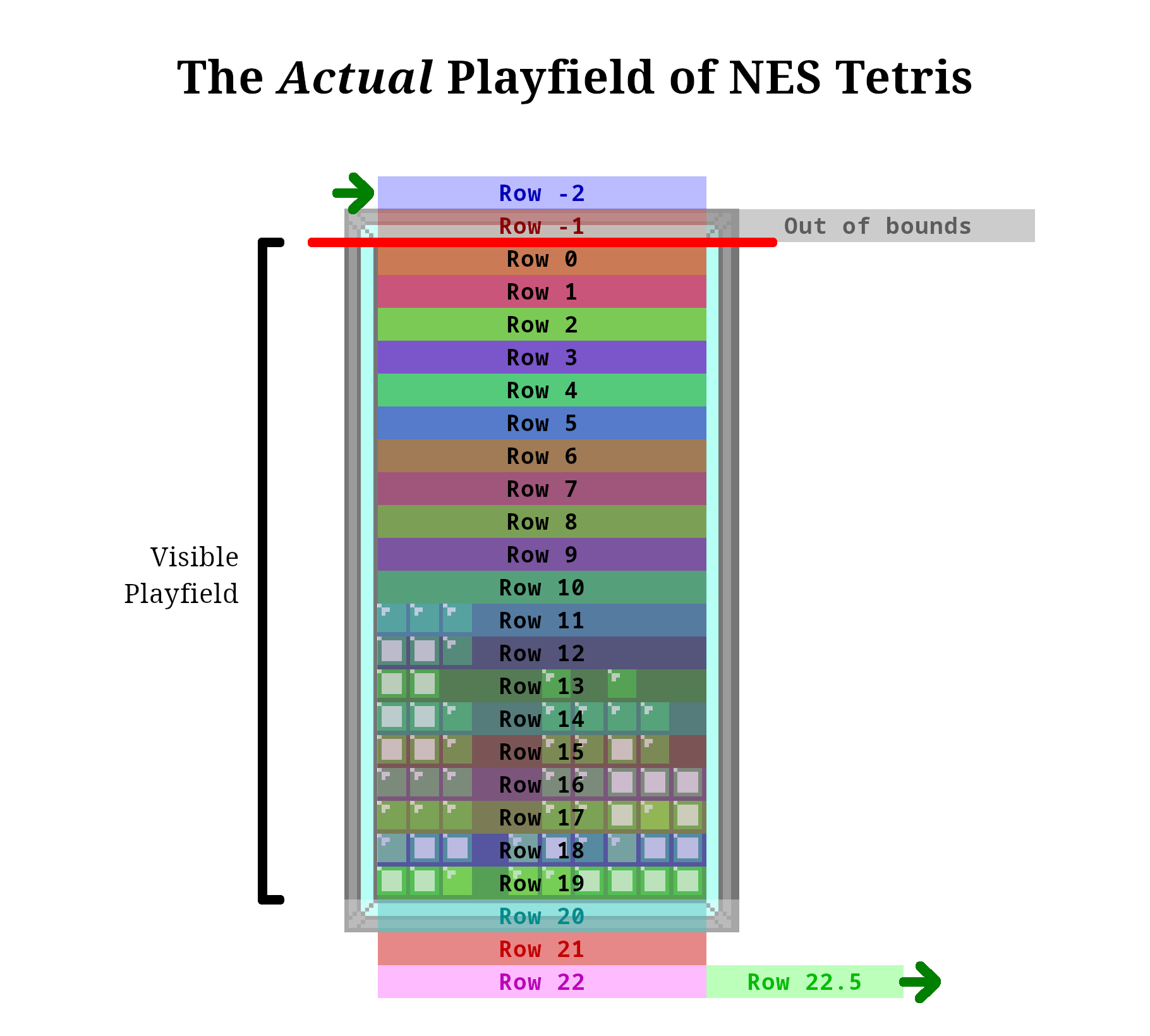
There's a slight problem with the storage method used above. When shifting or rotating the active tetromino, the game first checks whether the new position would collide with any non-empty tiles on the board. If it would, the move is deemed illegal and not performed. The board index to check is calculated by multiplying the row by 10 and adding the column, as one would expect. This is fine most of the time, but what if the tetromino is at the very top of the board, when it first spawned? At this point, certain tetrominos can be rotated, so they partially extend above the visible playfield. But what happens when the game checks if the rotation is legal? Since some of the tetromino now exists above row 0, the game checks for the index in row -1 (and possibly -2 for an "I" piece). But the indices aren't actually signed; they're unsigned bytes. So row -1 actually is checked starting at index $F6 (246).

This is a pretty big problem, right? Well, not really. Let's backtrack a bit. In the image above of board memory, you may have noticed that a lot more data is filled with $EF than just the visible playfield. This is because when the game starts, it actually initializes 256 bytes starting at $0400 to $EF. So the checks for rows -1 and -2 are actually perfectly fine; these "negative rows" are still part of the board array.

The board representation is quite wasteful with how much space is used, but things basically work as intended.

Clearing the top row

With very lucky RNG (or RNG manipulation), it's possible to clear the very top row of the board (row 0). What happens now? You may think that this just doesn't shift anything, and just empties the top row. That would make sense, and be consistent with the C code I used earlier.

Wait, what?

So, the C code above was a convenient lie. But the truth is more complicated.

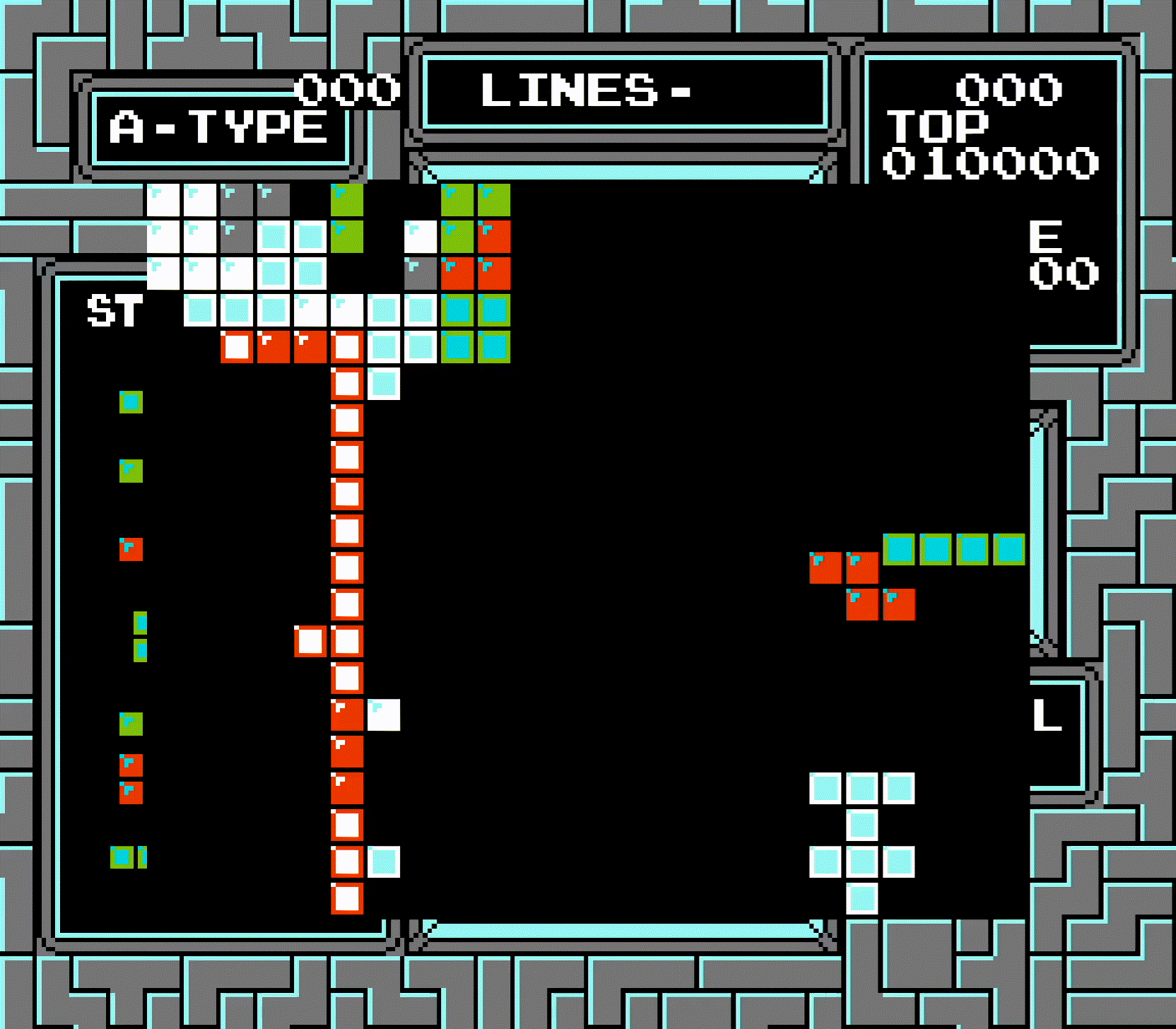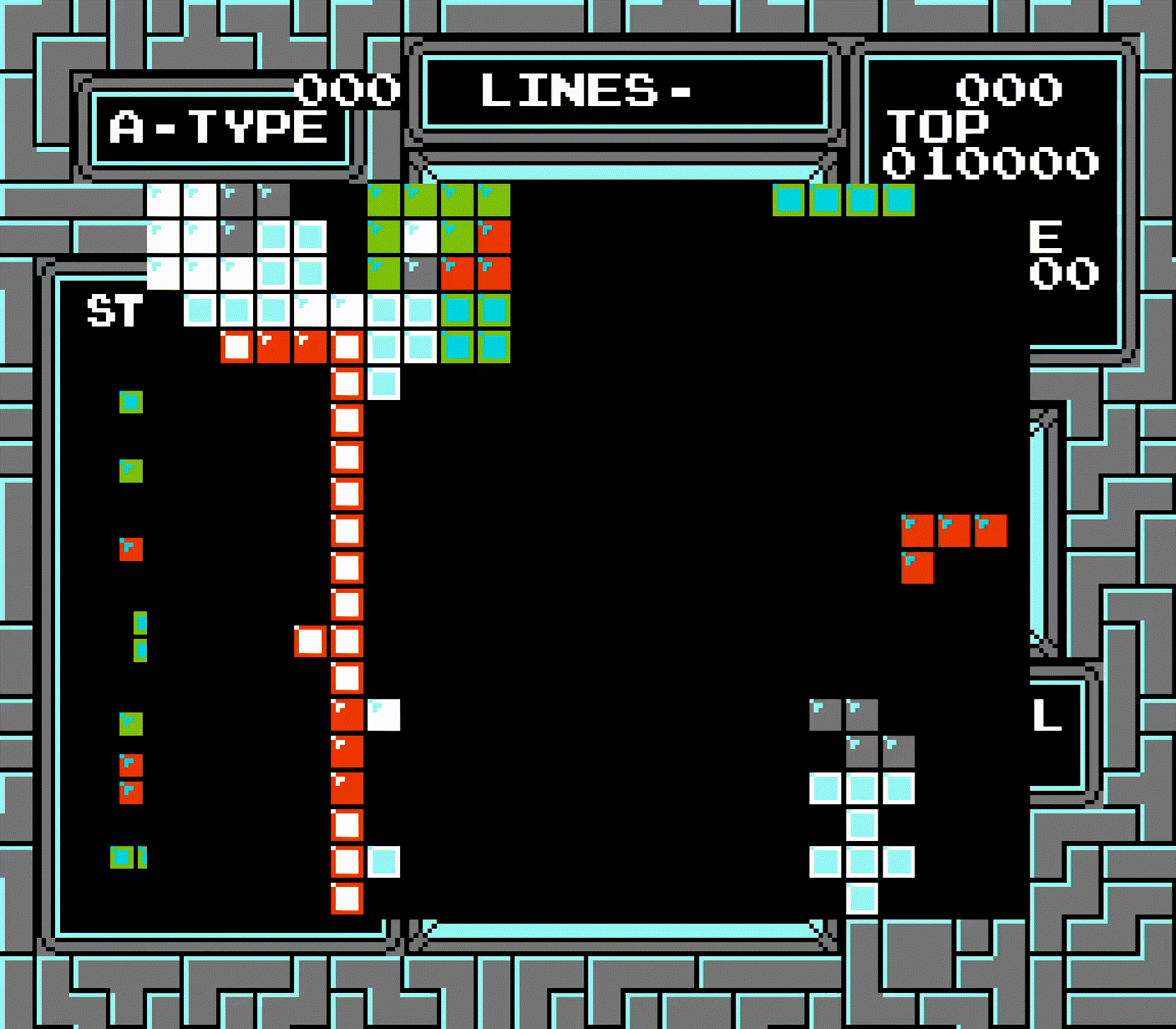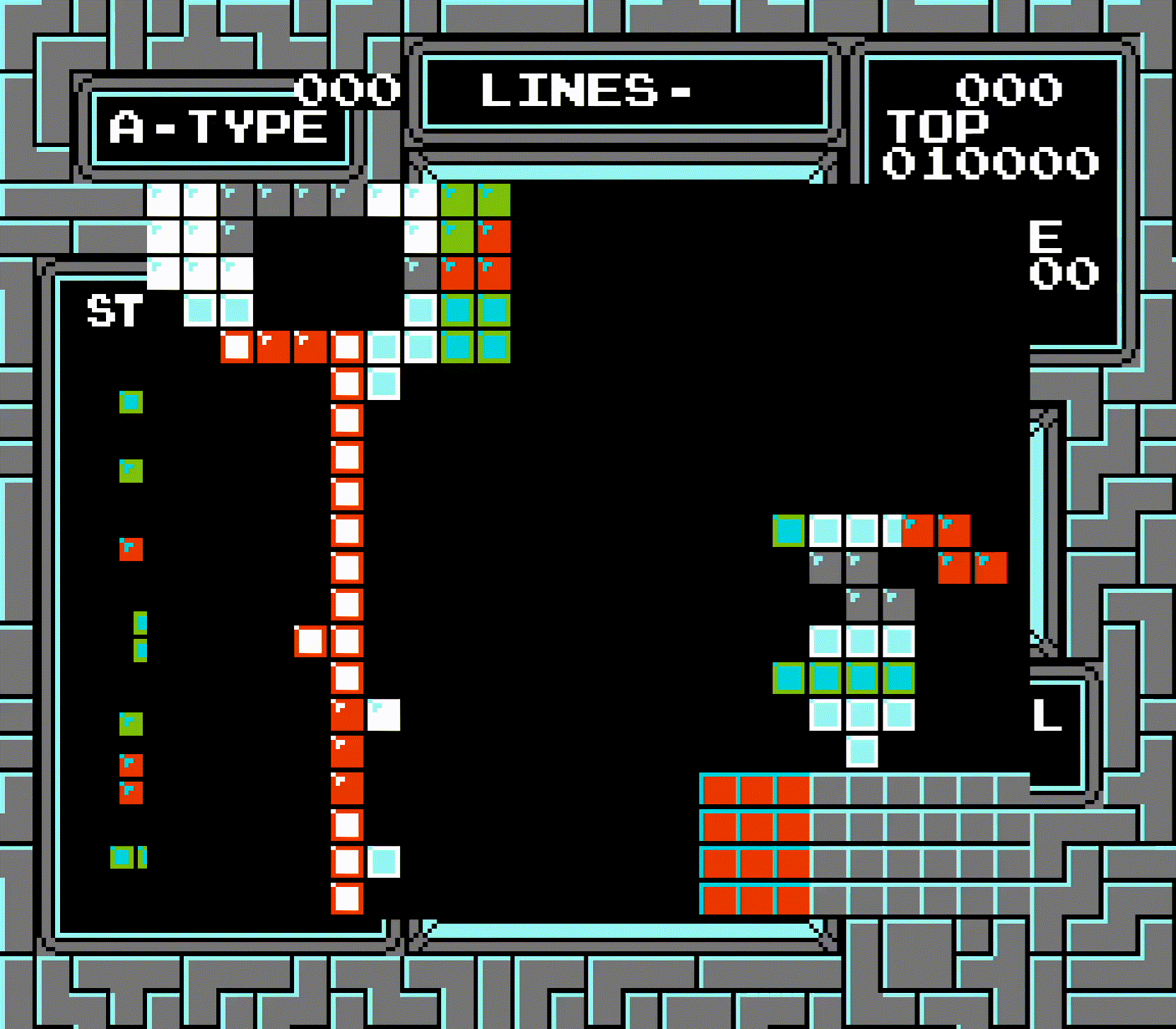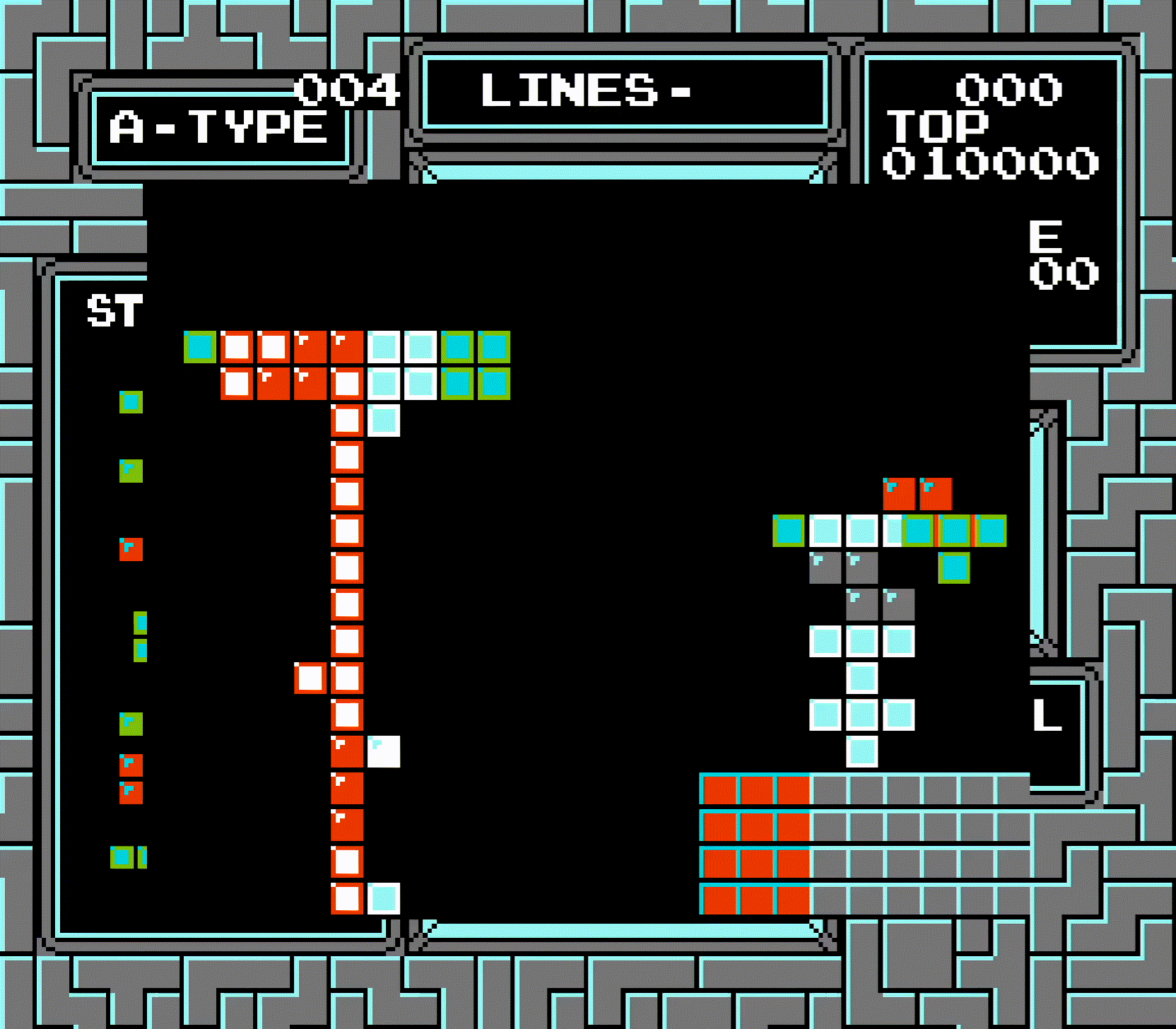
First of all, how are cleared rows even checked? When a tetromino locks, the game doesn't check the entire board; it only checks four rows, starting from two rows above the tetromino's center, and going down the board to one row below the tetromino's center. In normal play, this is enough to check all possible rows that could be cleared.

The center of the "I" piece is the bottom-center tile. Notice how the only rows that actually need to be checked are those ranging from two above to one below the center.

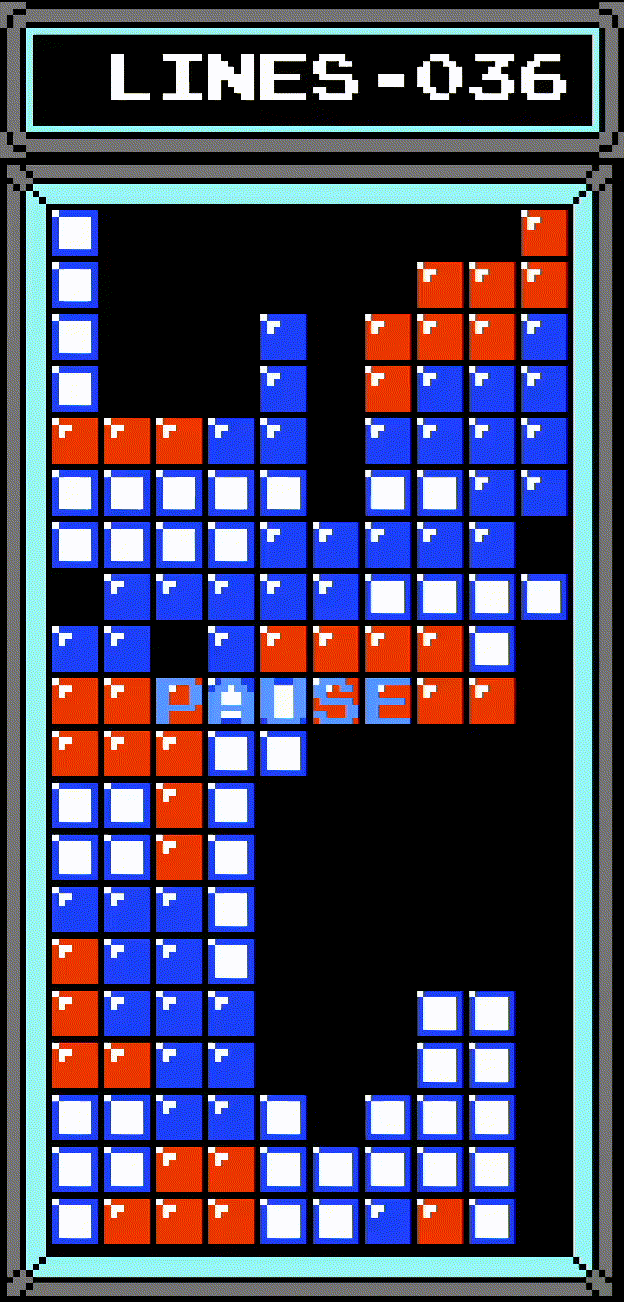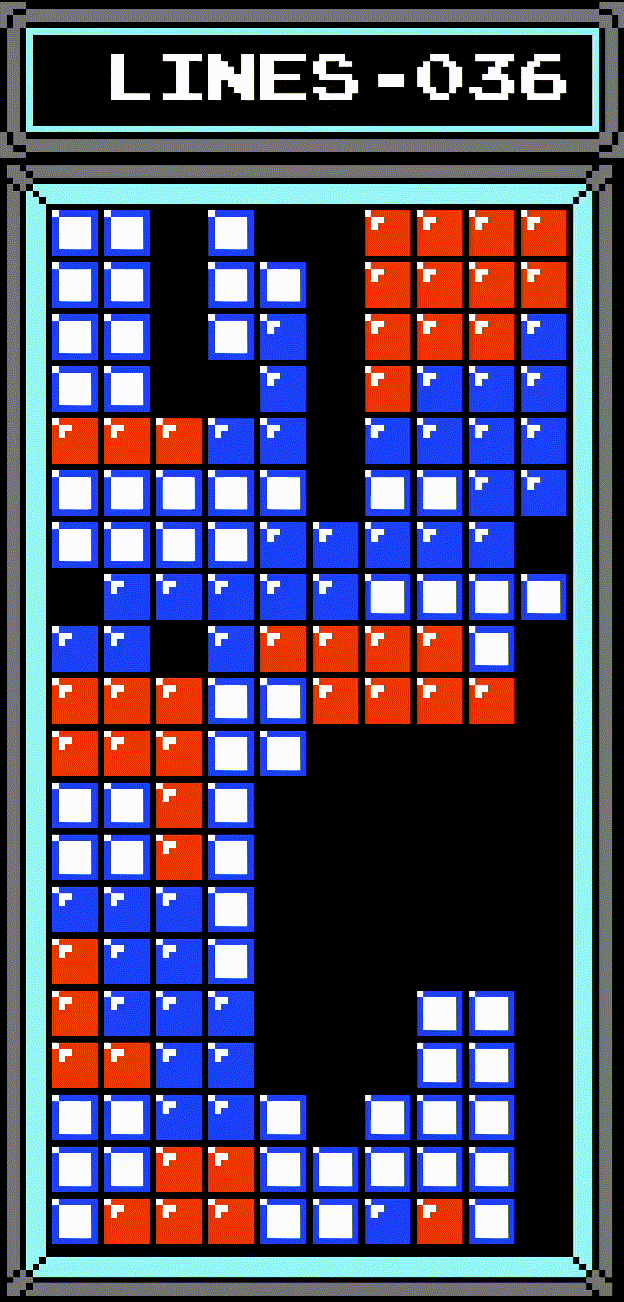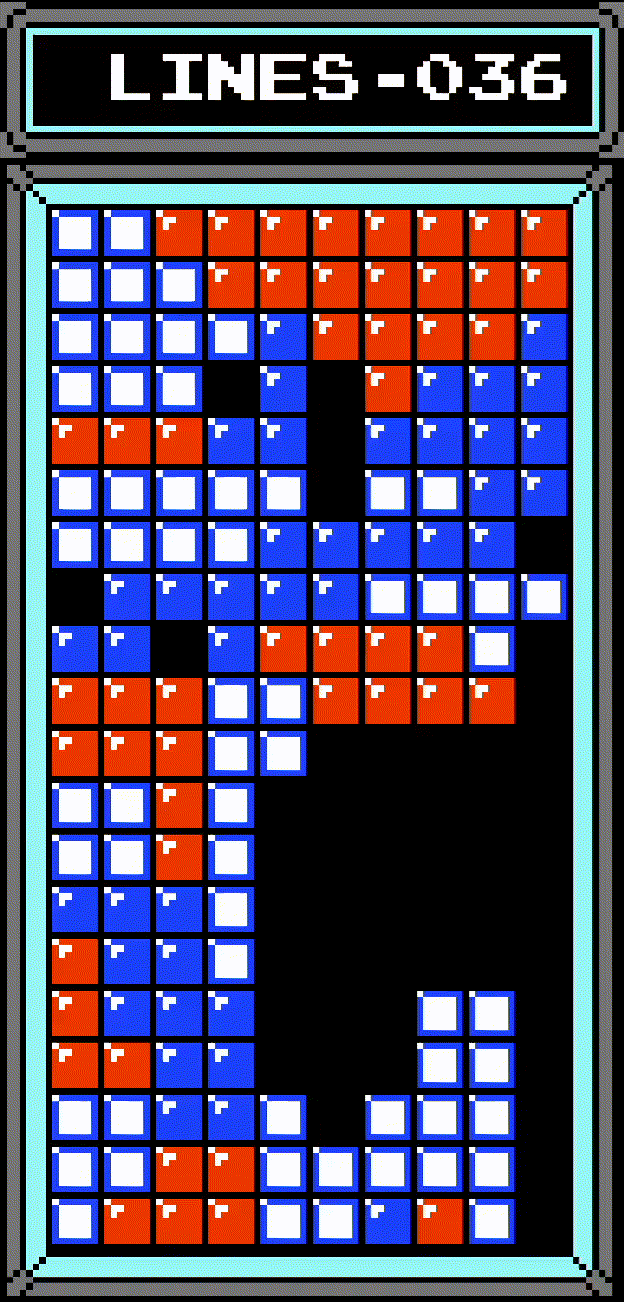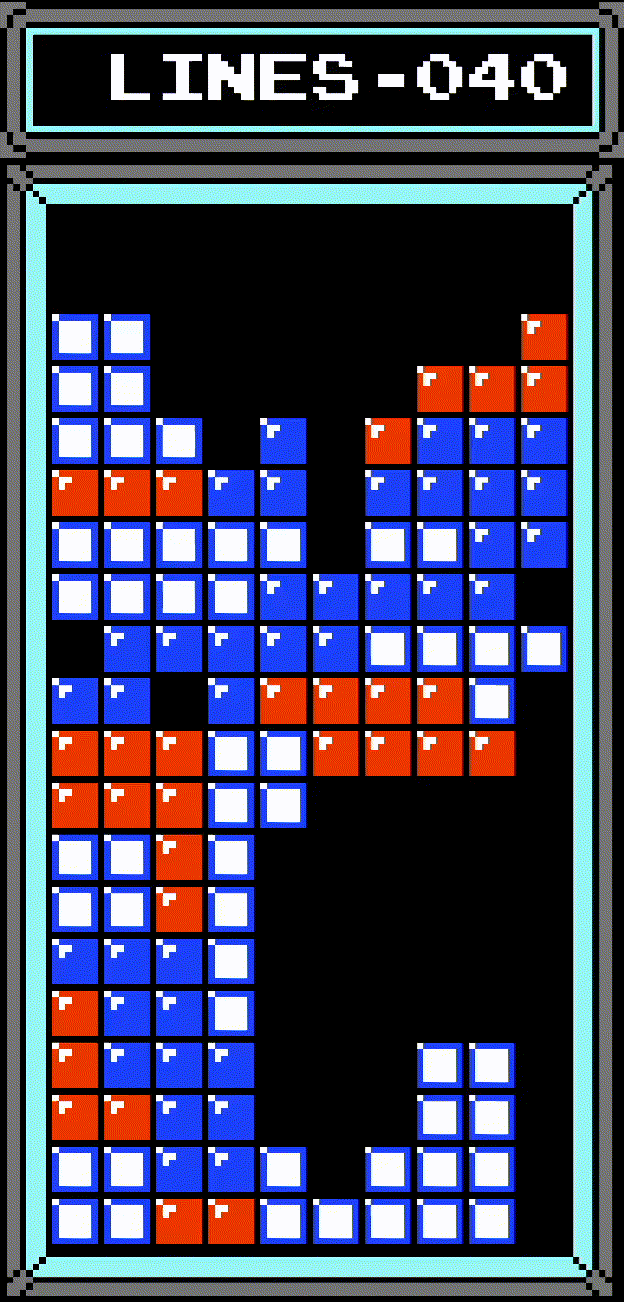
However, there's a few quirks here that I glossed over. These quirks all combine to create the bizarre behavior demonstrated above:

1. The first row checked isn't always two rows above the tetromino's center. If that row would be negative (or rather, greater than 127 if unsigned), row 0 is checked instead. I assume the intention of this was to ensure that rows not within the visible playfield aren't ever cleared, but the code was clearly never tested.
2. The shifting of board data doesn't have the same semantics as memmove. The developers incorrectly assumed that the amount of data being moved would never be zero, so the loop that shifts the data starts at index (row * 10 - 1), and ends when the index is zero. For the top row, this means looping through all 256 bytes of the board array.
3. In addition to shifting the board data, the index of the row that was cleared is also stored in $004A to $004D (i.e. there are four rows to check, the first check stores to $004A, the second to $004B, etc.) If the row wasn't cleared, 0 is stored instead. This data is accessed when drawing the line-clear animation
4. The shifting of the board data happens for every row cleared, i.e. when three rows are cleared, three separate shifts happen, each immediately after a row is checked. This was already established above, but it's worth reiterating. This is necessary because of split doubles/triples.

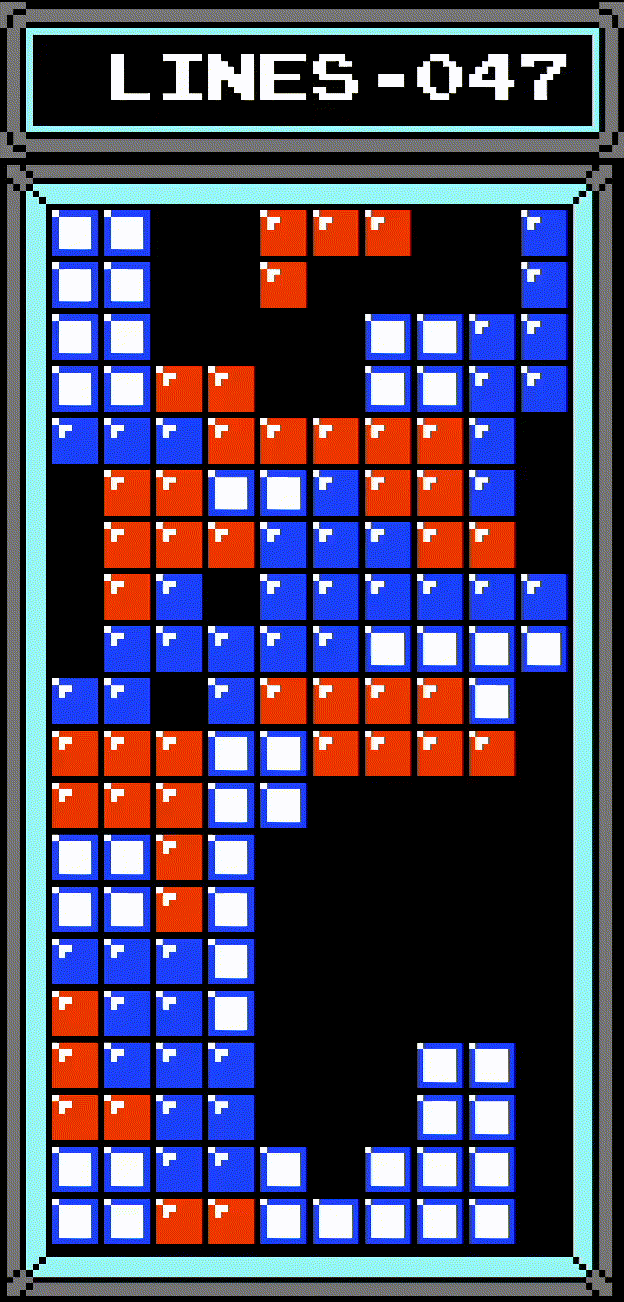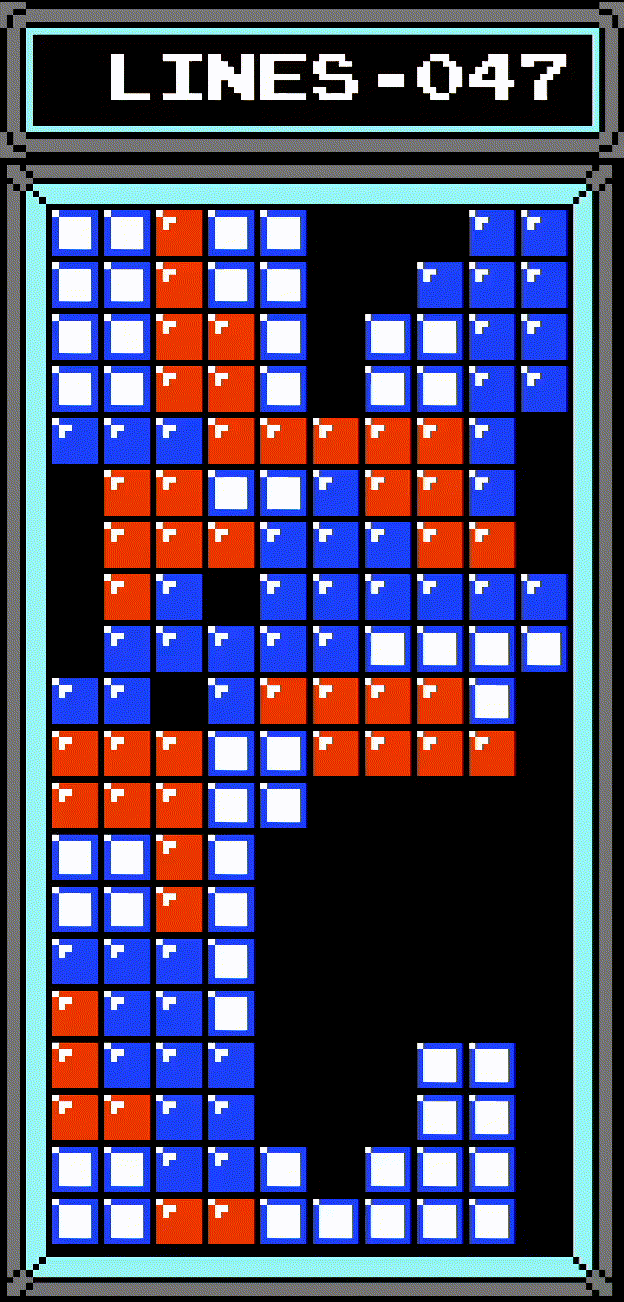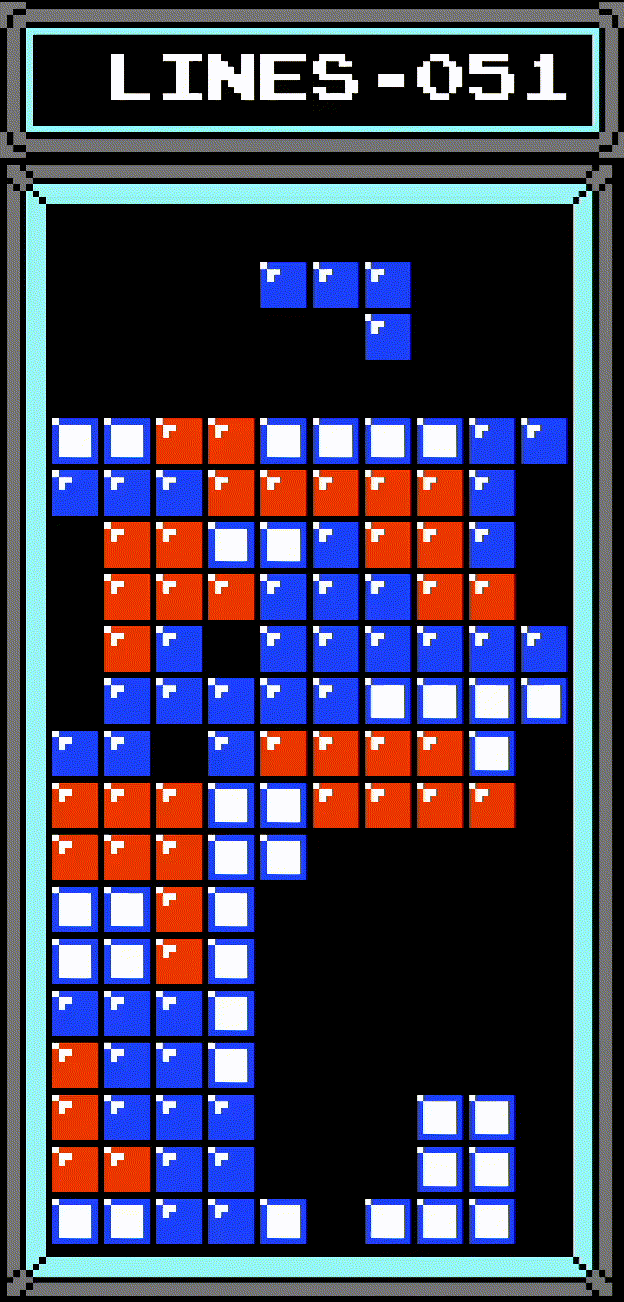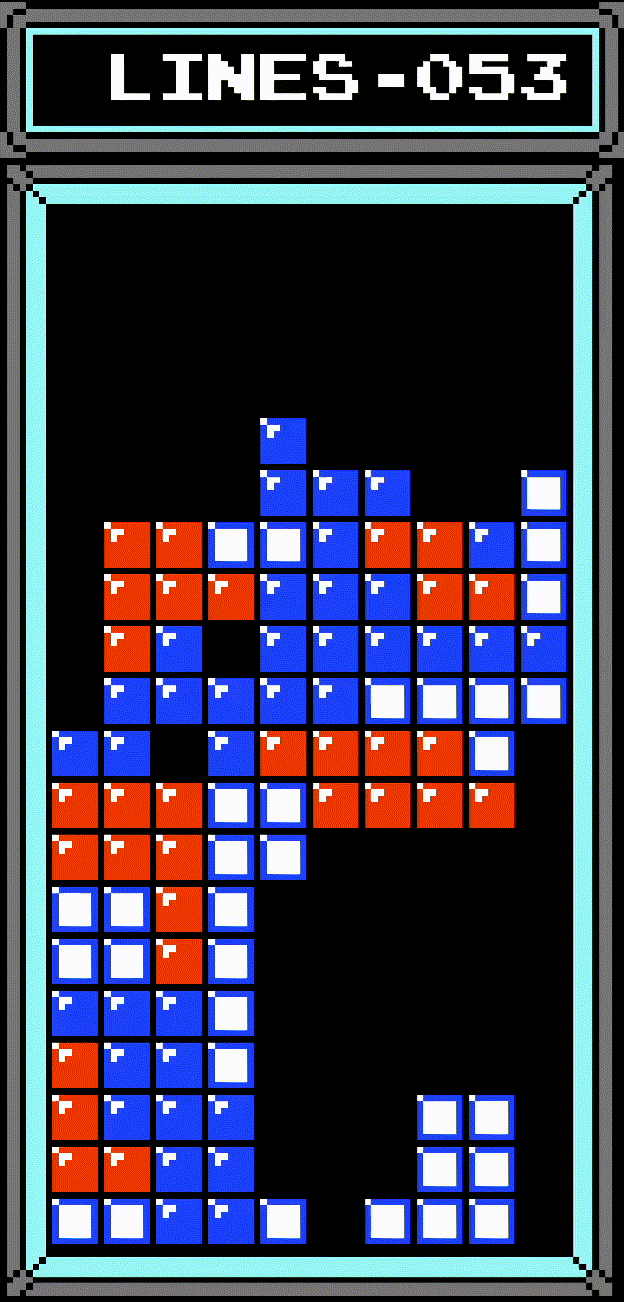
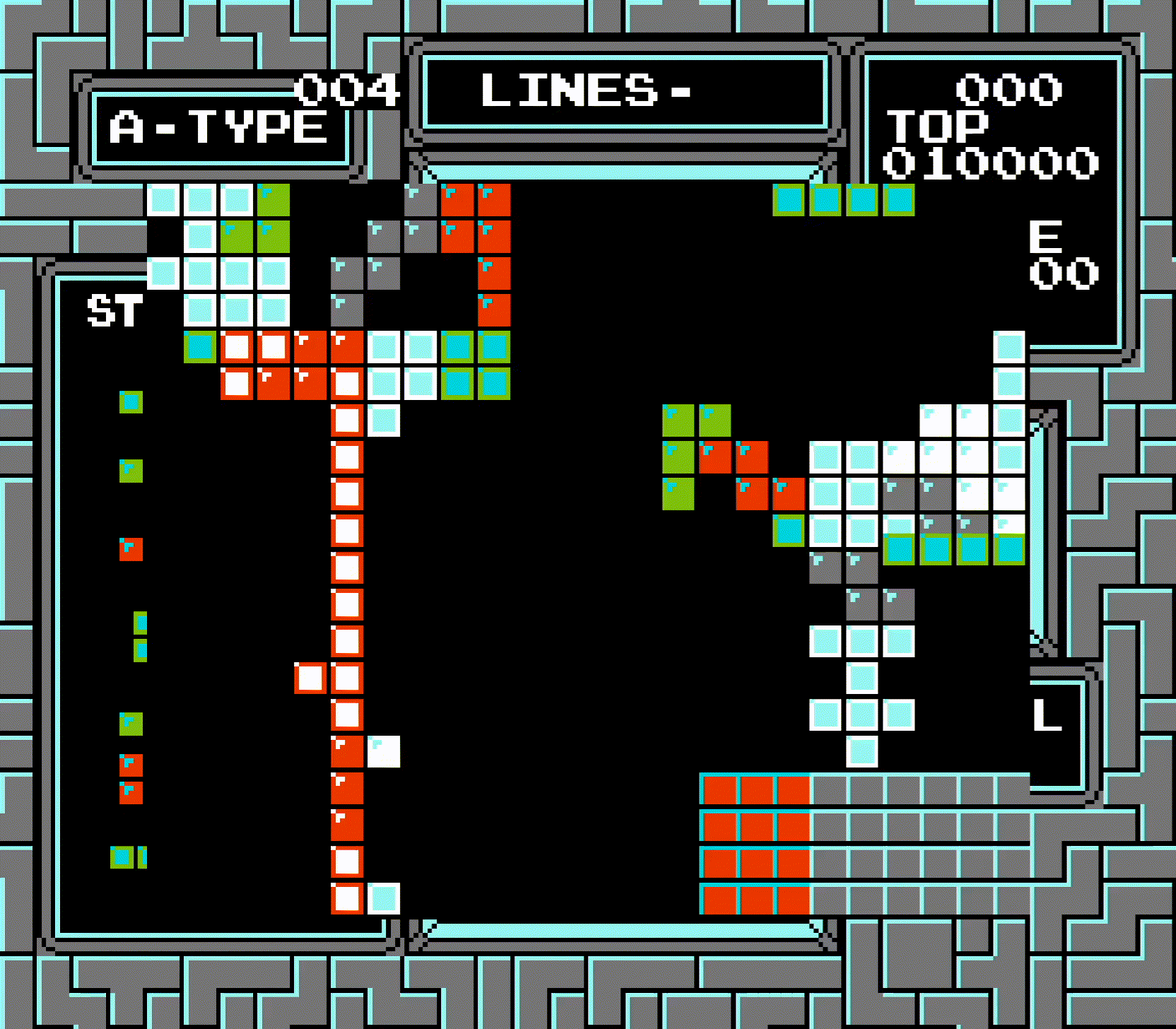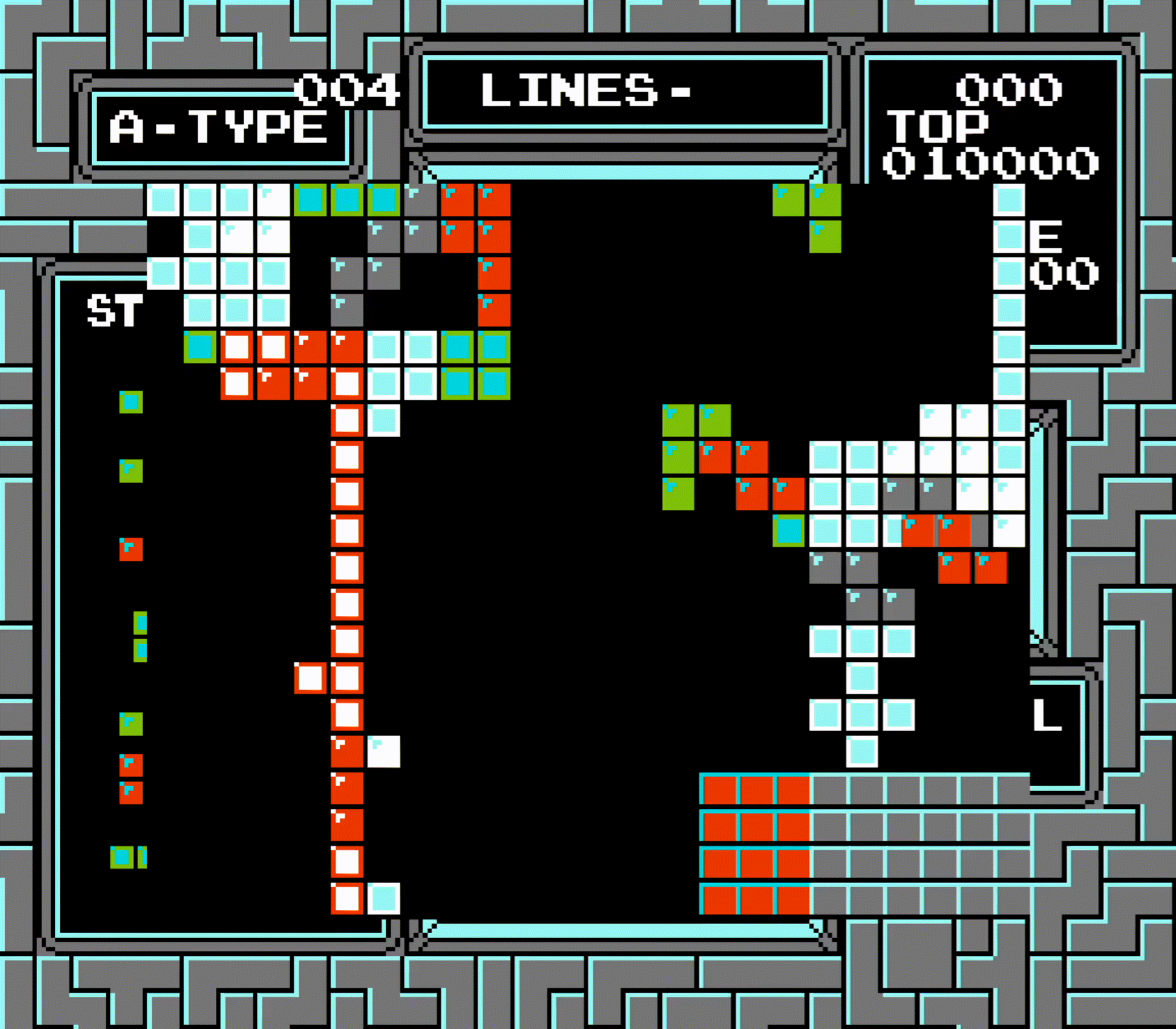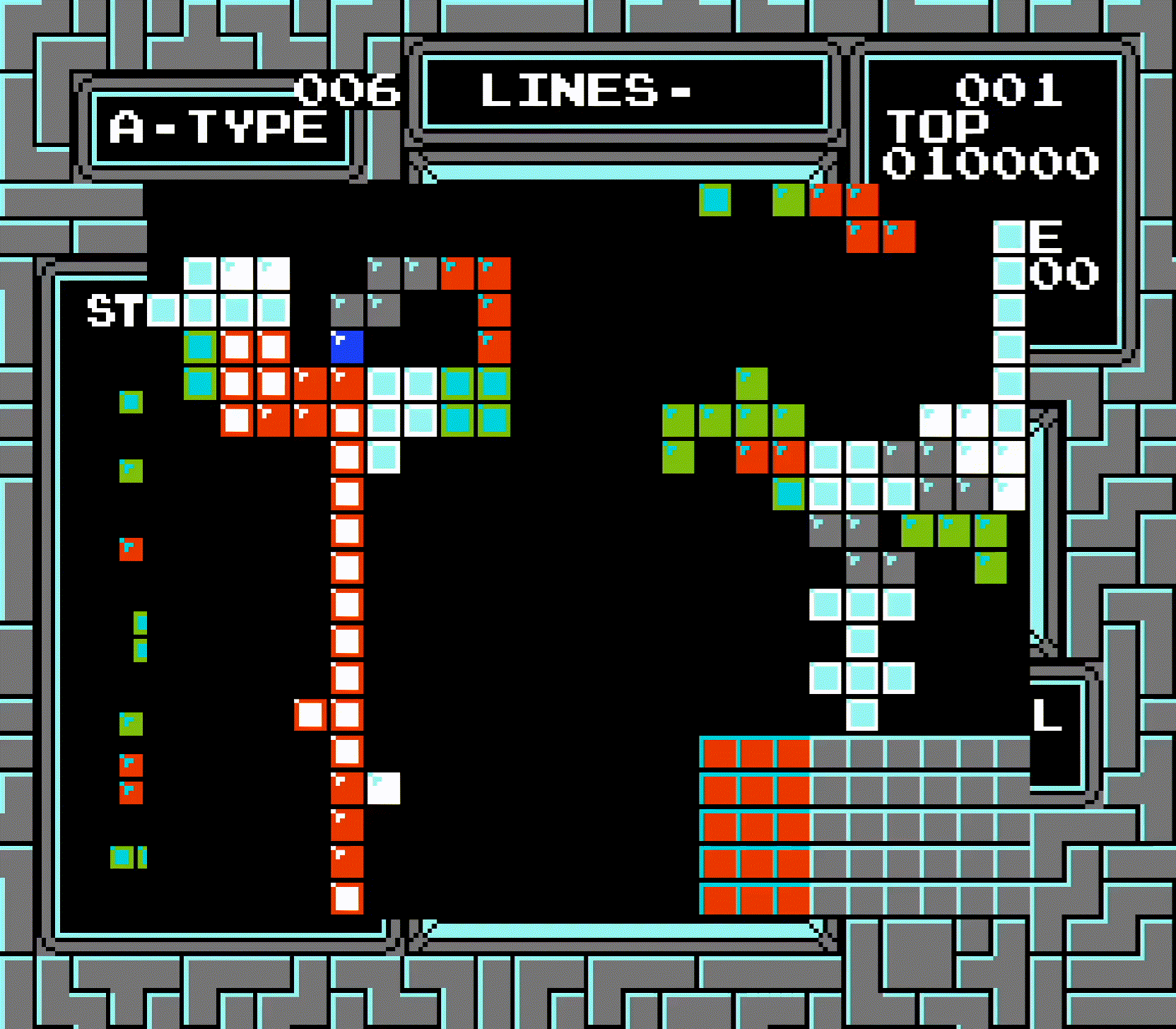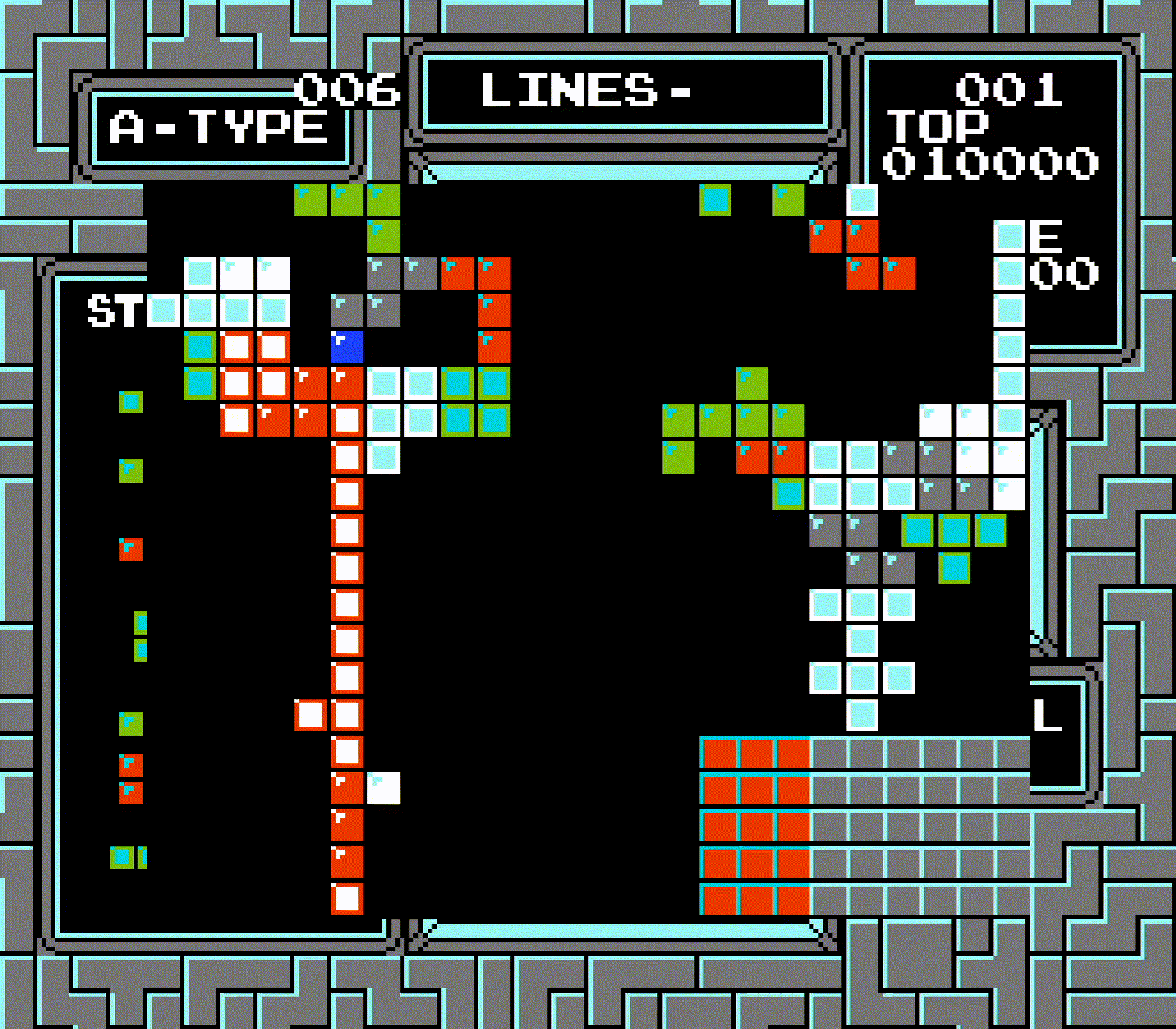
This may seem confusing, so let's walk through the animation of the triple at the top of the board step by step. First, we take the row that's two rows above the center of the tetromino. This ends up being one row above the top, so row -1. Per quirk #1, this is changed to row 0. So now, instead of checking rows -1 to 2, the game will check rows 0 to 3.

Starting with the check for row 0: the game recognizes that the line was cleared, so it shifts everything above it by 10. But, per quirk #2, the game actually moves all board data by 10. The result is the board is lowered by one, and the bottom row seemingly disappears. Finally, per quirk #3, the index of the row that was cleared is stored to $004A. But remember: an index of 0 means that the row wasn't cleared. So the line clear animation doesn't show row 0 as being cleared, even though it actually was.

Next, row 1. But wait, the entire board was just shifted by 10! Since the row that was checked last time has been shifted, this will end up checking the same row again! This time, however, the board shifting and the storing of the row index actually works correctly.

This is then repeated for rows 2 and 3, both of which work the same as row 1. Because the top row was effectively counted twice, what should've just been a triple is instead seen as a Tetris. The line clear animation can't distinguish between "row not cleared" and "row 0 cleared", so it doesn't show row 0 being cleared, but does show rows 1-3, which looks very bizarre. And of course, the entire board being shifted means the bottom row also disappears.

Here's another interesting side effect of these quirks: when a Tetris is scored at the top of the board, the bottom-most cleared row will never be checked, due to the board being shifted. As a result, it's possible to create a completed row that's not cleared by the game:

As demonstrated, this row can be cleared by certain tetrominos by laying them flat, since the row is exactly one row beneath the center of the tetromino.

Phew! Glad all of that is done. Well, there you have it, everything you need to know about NES Tetris' playfield.

jk there's more lol

What the hell even is a row

You may have realized I've been saying that the board data is shifted by 10, rather than just saying it's lowered by one row. Technically, yes, everything is shifted by 10, but isn't it more concise to just say things are lowered by one row? Well, I deliberately avoided saying this, for reasons that will hopefully make sense by the end of this section.

To begin with, let's debunk a misconception repeated in Applying Artificial Intelligence to Nintendo Tetris. To be clear, this is in almost all ways a great article (and is mostly completely unrelated to applying artificial intelligence to NES Tetris). This has been an invaluable resource for me when learning about NES Tetris' mechanics, and even for parts of this article. However, one bit of information seems to just be incorrect:

A piece can be locked in place such that some of its squares end up in negatively numbered rows without ending the game; however, in Nintendo Tetris, negatively numbered rows are an abstraction that only applies to the active Tetrimino. After a piece is locked, only the squares in rows 0 and above are recorded in the playfield. Conceptually, it is as if the negatively number rows are automatically cleared after lock occurs. But, in reality, the game simply doesn't store the data, potentially truncating away the upper part of pieces.

This is false. If a piece protrudes into negative rows, the data is stored. When the top line is cleared, this data may be shifted out of bounds, effectively "clearing" the row, but otherwise, the data stays there. This is relevant since, as briefly mentioned earlier, this data is checked by the game when attempting to shift or rotate a tetromino. When rows -1 and -2 aren't completely empty, certain shifts and rotations at the top of the board will stop working for seemingly no reason.

So, one way to populate rows -1 and -2 with non-empty tiles is to rotate pieces at the top of the playfield so they lock into place partially extending outside the visible playfield. But another way is to just continuously clear row 0.

When row 0 is cleared, all board data is shifted by 10. This includes the bottom row (row 19). Even though it looks like this row just disappears, it actually still exists, but beneath the visible playfield. Within "row 20", you could say.

As the top line is cleared again and again, the board data continues to shift, until eventually it "wraps around" to the negative rows. This is a bit misleading, since no data is actually being wrapped around. Rather, the negative rows weren't ever really negative to begin with: they were just grabbing data from the very end of the board array. But notice how the size of the array (256) isn't evenly divisible by 10. This results in rows being split up, so what eventually ends up at row -1 wasn't ever actually a row on its own to begin with; it's just two rows sliced and glued together. Maybe this diagram will do a better job of explaining this:

Note that I'm not representing any negative rows less than -2, since they can't be interacted with. Also, again, the negative indices aren't actually negative, but in my opinion it makes more sense to treat them as though they are.

It follows that it becomes more difficult to clear the top row after you've already done it five times or so, since you can no longer rotate or shift pieces as freely.

Wait what was that thing about out of bounds?

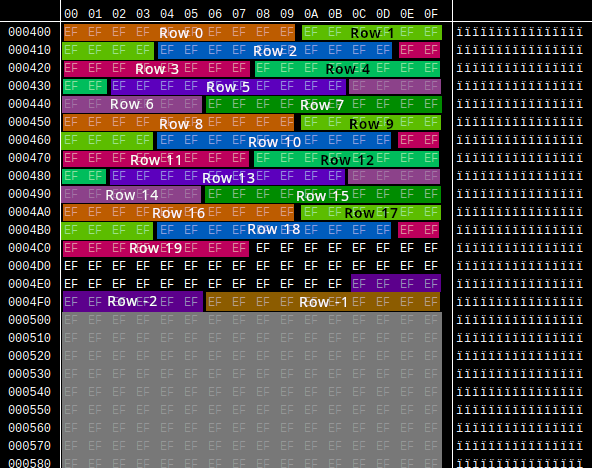
Yeah, I've been conveniently glossing over the fact that this is absolutely writing past the end of the array. More specifically, up to ten bytes after the board array (starting at $0500) may be written to. What's actually being stored here?

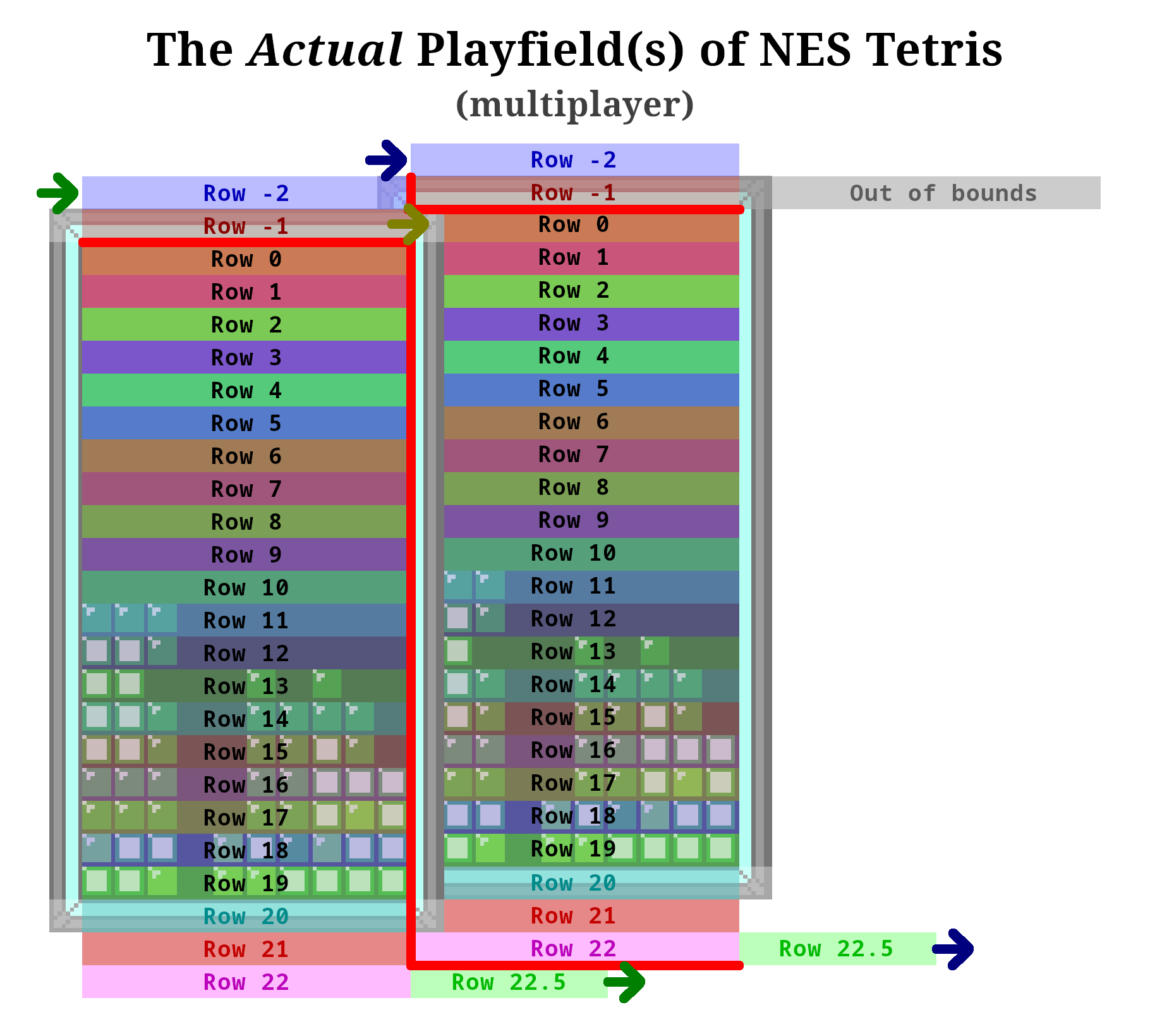
In the images of the hex editors, you may have noticed that all the grayed-out bytes are also $EF. That's because there isn't actually only one board. There's two, the second one stored at $500 immediately after the first one. This is for the 2-player mode that was scrapped late in development, so for unmodified gameplay, this memory is just unused. But just for fun, let's use the ZAUAPPPA Game Genie code to enable multiplayer, and watch what happens when player 1's board data is written out of bounds into player 2's board. Keep an eye on the top of player 2's board, it happens fast!

The board is only redrawn when a tetromino is locked, so I timed the inputs so player 2 locks a tetromino immediately after player 1 does, causing the overflown tiles to be drawn. However, clearing anything more than a single will send garbage to the opponent's board, which pushes the entire board up, discarding the top row. Since clearing the top row always registers at least a double, these tiles are very quickly overwritten with $EF once the game generates the garbage, which is why the tiles appeared so briefly.

That being said, until garbage is generated, the tiles really do exist on player 2's board, even if they aren't visible. We can use this, as well as the fact that line clears are processed before garbage, to keep the tiles on the board by having player 2's locked tetromino also clear a row:

So the playfield diagram can actually be updated for multiplayer mode, showing that the two boards are actually partially connected to each other.

As for me, after discovering this, I immediately checked what the memory stored immediately after player 2's board was being used for. Can we do anything interesting here? Sadly... I don't think so. The memory at $0600 is filled with zeros, and it looks like it just remains unused. So this sadly doesn't open up any exploitable vulnerabilities or anything like that. I guess that's a good thing for me, since it means I can implement this behavior in its entirety for generic tetromino game, without needing to embed a 6502 emulator and a full NES Tetris ROM.

Conclusion??

NES Tetris is fun and also completely broken and we love it for that. Also holy hell I have a lot of work to do for generic tetromino game.

Anyways yeah this has basically zero impact on how Tetris will play for almost all human players, but this stuff is still fascinating regardless. something something i suck at endings, thanks for reading! :)